前回の記事→> 【物理徹底解説】力学単振動を完全攻略①～公式チェック編

前回の記事に引き続き、おそらく多くの人が苦手とする分野であろう単振動の解説をしていきたいと思います。私も受験生だったとき単振動が苦手だったのですが、あるとき解き方のコツをつかみ単振動の問題が得意になりました。なので、単振動が苦手で解き方がわからない！という人はぜひこの記事を読んでみてください！
今回の記事ではいよいよ単振動の問題の解き方を解説します！ですがその前に前回の記事の細かい補足を二点させていただきます！
まず一点目。前回の記事では単振動の運動方程式はF=-Kxだとしました。しかし、実はそれは正確ではありません。正しい単振動の運動方程式は、
F=-K(x-x₀)  (x₀は振動の中心座標)
となります！どういうことか、代表的な単振動であるバネの運動を用いて説明します。

　
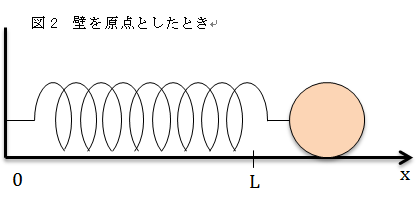
図1と図2を見てください。二つの図は両方自然長L、ばね定数kのばねに質量mのおもりがついている状態です。ただし、図1ではx座標の原点がばねの自然長なのに対し、図2では原点が壁になっています。このとき、おもりについてx軸方向の運動方程式を立てると、図1ではma=-kxとなりますが、図2ではma=-k(x-L)となりますね。そしてこれが何を表すかというと、図1ではx=0を中心に単振動するのに対し、図2ではx=Lを中心に単振動するということです!つまり、運動方程式を立てることで角速度や周期だけでなく振動中心の座標もわかるのです！

二点目の補足は、単振動の座標の式です。前回の記事ではx=Asinωtとしましたが、これはt=0の時にx=0となる単振動の場合だけです。より正確な式は
x=Asin(ωt+φ)  (φは初期位相)
となります。初期位相とは、単振動に対応する等速円運動でのt=0での角度だと考えてください。例えば、バネをのばした状態から離したときの単振動を考えてみましょう。対応する等速円運動でのt=0での角度はπ/2となるので、座標の式はx＝Asin(ωt＋π/2)=Acosωtとなります。（自分で図を描いて考えてみましょう！）

ではいよいよ問題に入りたいと思います！まずはこの問題です！

単振動の例題１

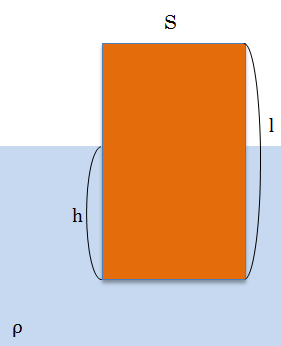
①長さl、断面積Sの木を密度ρの水に浮かべたら、hの深さで静止した。そして少し押して放すと振動を始めた。ただし、水の抵抗はないものとする。
(1)木の密度を求めよ。
(2)振動周期を求めよ。

単振動例題１の解答

(1)まずは静止したとあるので力のつりあいを考えてみましょう。木の密度をρ₁とすると木の質量はm=ρ₁であり、静止した状態で受ける浮力の大きさは浮力の公式f=ρVgより、ρShgとなります。よって、重力と浮力のつりあいより
ρ₁Slg=ρShg　　　　　　　　∴ρ₁=hρ/l
(2)

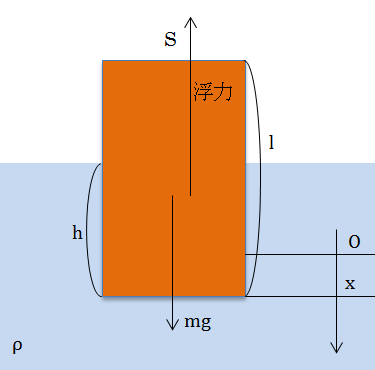
単振動の問題では、まずは座標xが含まれる運動方程式を立てましょう！x軸はどのようにとってもいいのですが、今回は静止状態での木の底面の位置を原点として下向きにx軸をとってみましょう。木の底面が位置xに来た時に受ける浮力の大きさはρS(h+x)gとなるので、運動方程式は
ma=ρ₁Slg-ρS(h+x)g=ρShg-ρS(h+x)g=-ρSgx
ここで、単振動の式F=-K(x-x₀)と見比べると、この木は振動中心x=0、比例定数K=ρSgの単振動だと分かります。したがって振動周期は、

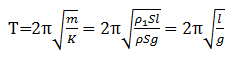
となります。
この問題のように単振動はばねに限りませんが、振動周期とか言われたらまずは運動方程式を立てるようにしましょう！

では次の問題です。この問題は少し難しめですよ！

単振動の例題２

②傾角30°の滑らかな斜面上で、ばね定数k、自然長Lのばねに質量mの大きさの無視できるおもりを結び付け、自然長の位置(x＝L)で初速度v₀を与える。

(1)単振動の周期Tを求めよ。
(2)単振動の振幅Aを求めよ。
(3)運動開始時からおもりが初めて振動中心を通るまでの時間がT/3だったとする。この時のv₀を求めよ。

単振動例題２の解答

(1)ばねなので当然なのですが、次の問題ので振動中心を知る必要があるので一応運動方程式を立ててみましょう。おもりの位置がxのときの運動方程式は、
ma=-mgsin30°-k(x-L)=-k(x-L)-mg/2=-k(x-L+(mg/2k))
よって、周期T=、振動中心L-(mg/2k)の単振動をします。

(2)振幅を求めるときはエネルギー保存則を使うことが多いです。運動開始時のエネルギーと振動の端にいるときのエネルギーを比較すると、運動開始時の振動中心との距離はL-(L- mg/2k)=mg/2k、振動の端にいるときの振動中心との距離はAなので、

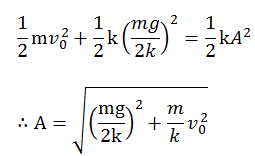
ここで、重力による位置エネルギーはいらないのか？と思う人もいるかもしれませんが、自然長からの伸びではなく振動中心からの距離を考えた時の単振動の位置エネルギーには重力の位置エネルギーも既に含まれているので気を付けてください！
(3)さて、この問題は式で考えてみてもいまいちピンと来ないかもしれません。そういう時は、図を描いて考えてみましょう！

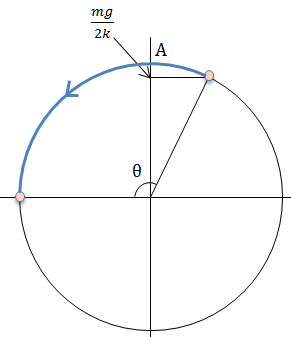
今回の単振動と対応する等速円運動は次の図のようになります。すると、青い弧の長さが円周の1/3になればいいので、θ=2π/3となればいい。よって、

今の2問、皆さんは解けたでしょうか？基本的に単振動の問題は、周期や振動中心を知るために運動方程式をかく、振幅や速度を求めるためにエネルギー保存則を解くことが基本となります。受験頻出の分野なので絶対にできるようにしておきましょう！

この記事を読んで物理の勉強が必要だなと感じた人は以下の記事で私がほぼゼロの状態から東大合格レベルまで成績を伸ばすことができた物理の勉強法と参考書について紹介ししているのでぜひ読んでください。

> 物理の成績を着実に伸ばすおすすめ参考書と3つの勉強法を現役東大生が解説しよう

大学受験生で物理を使う受験生におすすめの記事

> 【物理・力学編】公式一覧とその覚えるコツまで、これでアナタも力学マスター

合わせて読みたい

物理の成績を着実に伸ばすおすすめ参考書と3つの勉強法を現役東大生が解説！ 現役で東大に合格できたと聞くと、「どうせ高1の時からガッツリ勉強してたんでしょ?」と思われるかもしれませんが、実は私は高3生になるまではまともに物理の勉強をしていませんでした。

合わせて読みたい

[物理]ゼロから難関国公立に合格できる物理の勉強法を現役東工大生が伝授します 「物理の知識が完全にゼロ → 難関国公立大学に合格」を可能にする、物理の勉強法と参考書を紹介します。理系でも苦手な人が多い物理の悩みを完全に解決します。

合わせて読みたい

物理のあらゆる悩みを解決する、8人の難関大学生による22の勉強法とノウハウ 物理とはすべての根源となる現象を学ぶ科目と言っても過言ではありません。物理の記事を【一気通貫勉強法】【導入】【参考書紹介】【センター対策】【入試直前大学別対策】【その他】に分け、物理のオススメ記事をして紹介していきます。