前回は集合とは何かについて学習しましたね。今回は部分集合、共通部分、和集合、補集合についてです。まずは具体的な例でイメージしていきましょう。

-----------------------------------------------------------------------
前回読んでいない方はこちら↓
【独学生のための参考書！~数学 入門編~】  論理と集合  Part 1
-----------------------------------------------------------------------

<例>　ある高校のデータ

・全校生徒 1000人

・運動部所属　550人

・文化部所属  400人

・運動部と文化部を兼部している生徒　70人

部分集合

部分集合とはその名前の通り、ある集合の１部分の集合を表します。この例では、「ある高校に在籍する生徒」の集合をUとし、「運動部に所属している生徒」の集合をAとしたときにAを満たす生徒は全員Uを満たすといえます。このときAはUの部分集合であるといいます。図で表すと以下のようになります。

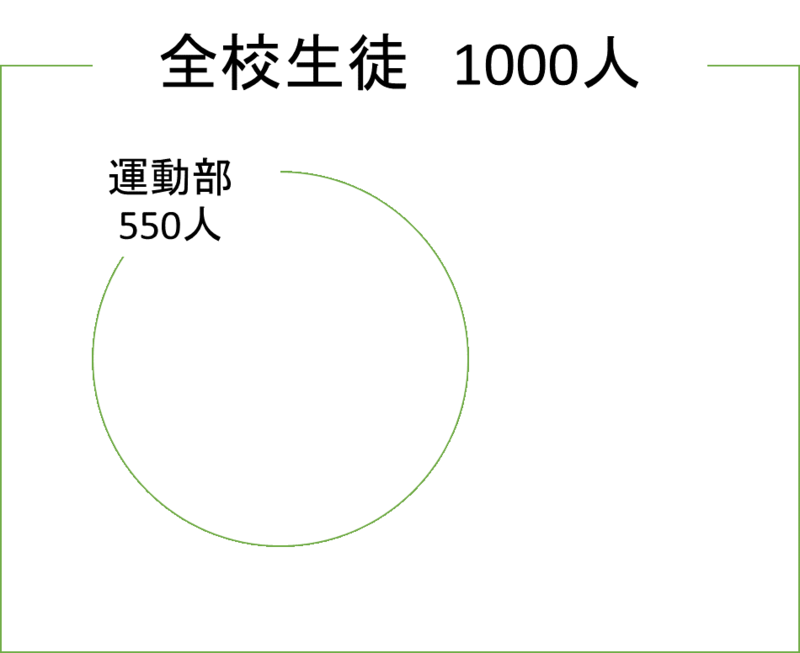
記号ではA⊂Uと表します。不等号と同じように大きいほうの集合に口が開いています。

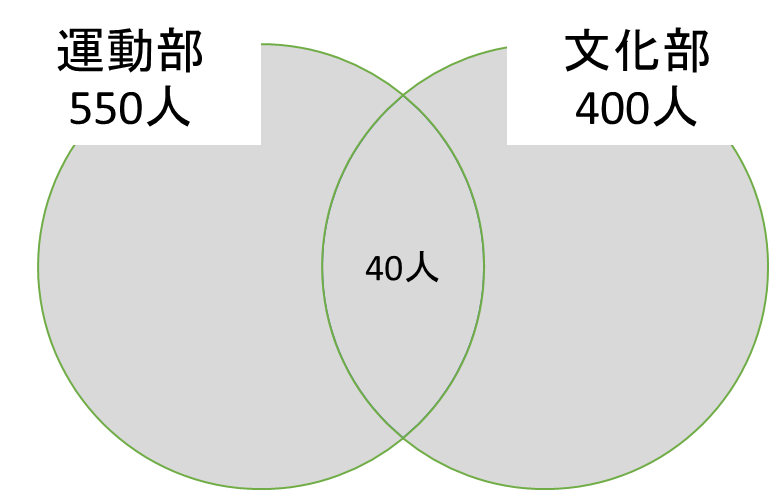
共通部分

共通部分も名前の通りです。2つ以上の集合の共通している部分です。この例では、運動部にも文化部にも所属している「運動部と文化部を兼部している生徒」にあたります。図で表すと下図のようになります。

数学的に表現していきましょう。「運動部に所属している生徒」の集合をA、「文化部に所属している生徒」の集合をBとします。このとき「運動部にも文化部にも所属している生徒」の集合はA∩Bと表します。

和集合

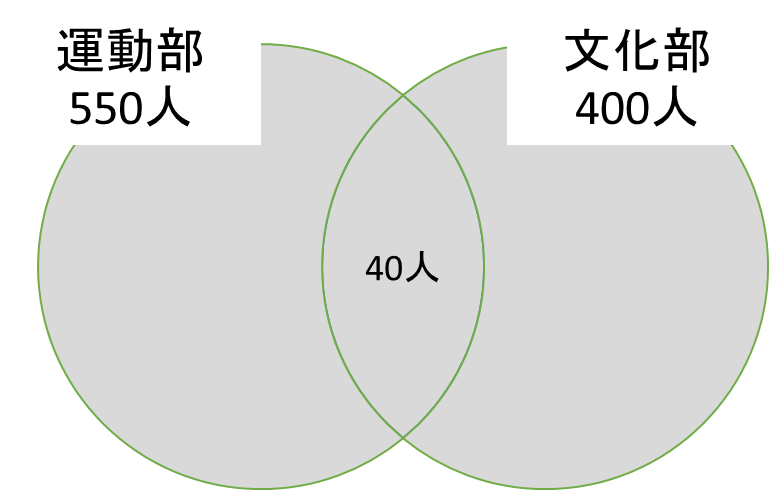
　和集合とは、”和”という言葉が表すように、少なくとも一つの集合に属する要素全体の集合です。この例では、運動部、文化部の少なくともどちらか一方に属している生徒全体の集合となります。今、アタマの中が???となっている人！図で見てみましょう。

なんとなくイメージがわいたと思います。こちらを数学的に表現すると「運動部、文化部の少なくともどちらか一方に属している生徒全体の集合」をA∪Bと表します。

では、上の例において運動部、文化部の少なくともどちらか一方に属している生徒は何人いるのでしょうか。550+400=950人でしょうか。いえ、違います。ここでは、兼部している生徒も考慮しなくてはいけません。正しくは、

550+400-40=910人

となります。

      　　          　= 　　　+　　      －　

ひょうたん           　　　=　あんぱん            ＋           あんぱん　－　かきのたね

Aの要素の個数はn(A)で表します。したがって上の絵を式で表すと

n(A∪B)=n(A)+n(B)－n(A∩B)

                                                          =550+400－40

                                                          =910

というように表します。

今回はここまでです。また次回も頑張りましょう！

【独学生のための参考書！~数学 入門編~】  論理と集合  Part3