今回は補集合とド・モルガンの法則についてです。聞きなれない言葉ですが恐れることはありません！先入観で嫌になってしまうことは禁物です。フラットな気持ちで読んでいきましょう！

―補集合―

教科書には、「ある一つの大きな集合U(全体集合という)を決め、その中のある部分集合Aについて考えたときに、Aに属さないUの要素全体の集合をUに関するAの補集合といい、で表す。」と書いてあるけど…

まずは、図で確認しましょう！

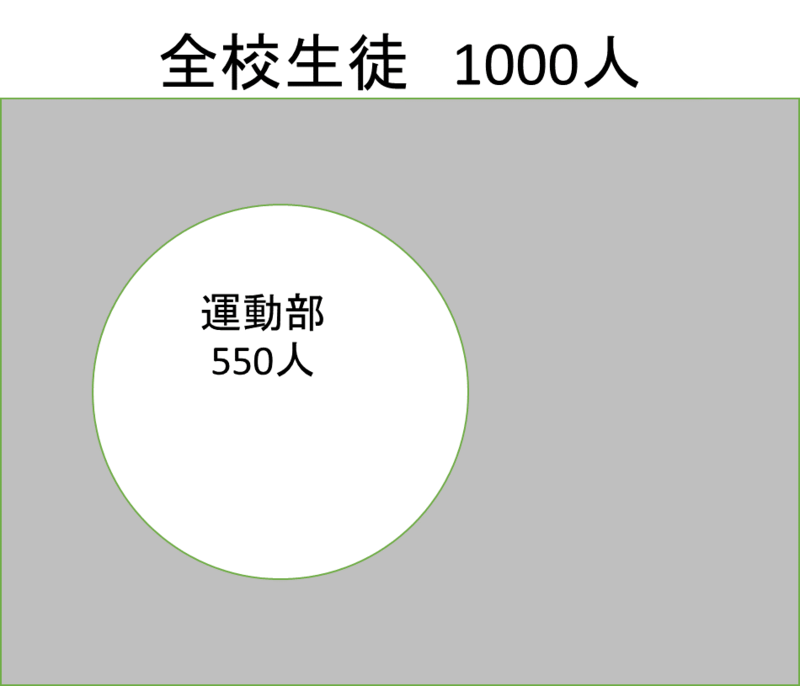
全校生徒(四角形で囲まれた集合)をU、運動部に所属している生徒(丸で囲まれた集合)をAとすると、色を付けた部分の集合は何になるでしょうか。この集合は、この学校の生徒のうち、運動部に所属していない生徒全体の集合になります。これこそ Uに関するAの補集合なのです。

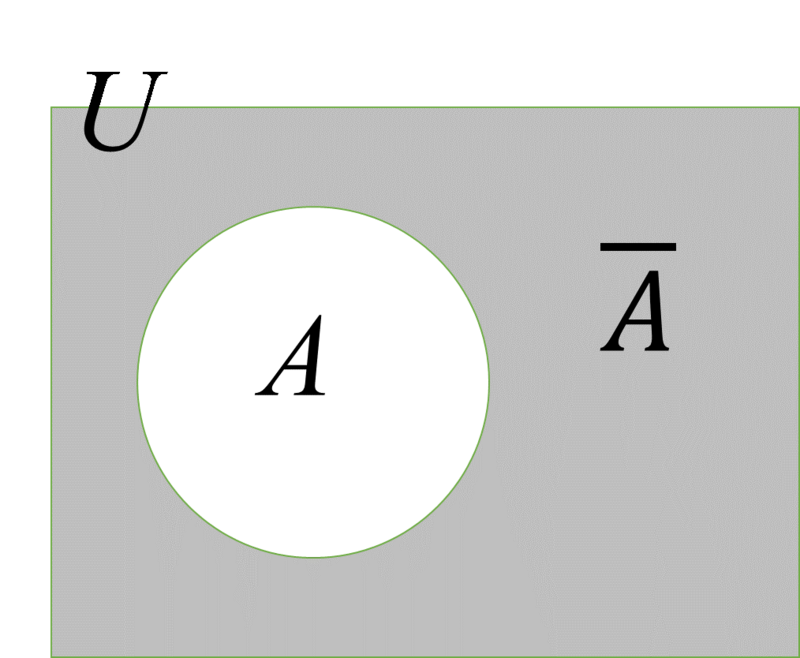
では、この学校の生徒のうち、運動部に所属していない生徒は何人いるのでしょうか。計算は簡単です。1000-550=450人です。これを数式で表すと、

                                                            =1000-550

                                                            =450

となります。

―ド・モルガンの法則―

名前は難しそうな感じしますが、そんなに難しくありません。まずはどんな法則なのか見てみましょう。

これも図でイメージすれば何もむずかしくありません。上の式について確認してみましょう。

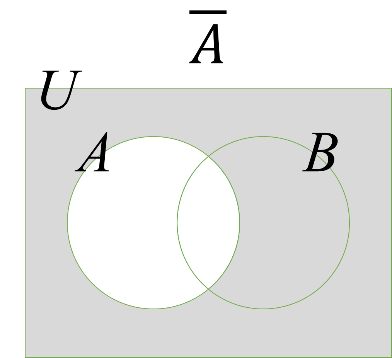
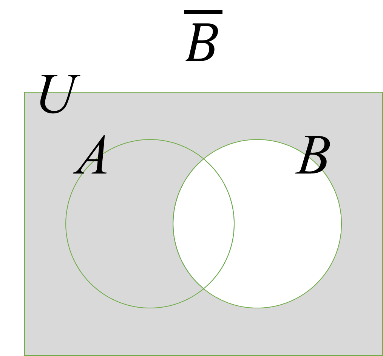
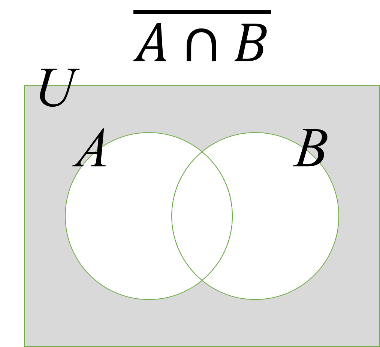
これでもえっ？と思う人がいたら、補集合を表す””や共通部分を表す”∩”の意味を確認しましょう！

Part1 : https://www.ikstudie.com/articles/183
Part2 : https://www.ikstudie.com/articles/186