こんにちは！みなさんは三角比と聞いてどんなイメージを浮かべますか？サイン、コサイン、タンジェントなんて言葉を浮かべる人が多いと思います。今回から数回にわたってこのサイン、コサイン、タンジェントがどのようなものなのかを学んでいきましょう！

三角比ってなに？記号の読み方をマスターしよう

サイン、コサイン、タンジェントとは簡単にいえば直角三角形の辺の比です。

上から

サイン、コサイン、タンジェントの定義です。sinの後のθ は角度を表していて、シータと読みます。この分野をはじめ、よく出てくるので覚えておきましょう！

sinとcosで何が違うのかが分かりづらいと思うので、cosがθを挟むと覚えておくといいと思います。

三角比のsin,cos,tanにはどんな相互関係が？？

今回は三角比でよく使われるsin,cos,tanの相互関係に関する式の紹介です。今回登場する３つの式は三角比にとどまらず、数学Ⅱの三角関数でも頻繁に使う式になるのでしっかり理解し使えるようにしましょう！

今回は前回出てきたsin, cos, tan の間にどんな関係があるのかを見ていきましょう！
まずは定義のおさらいです。

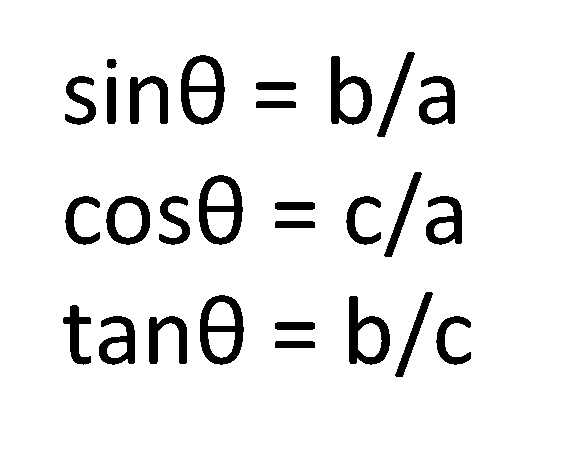
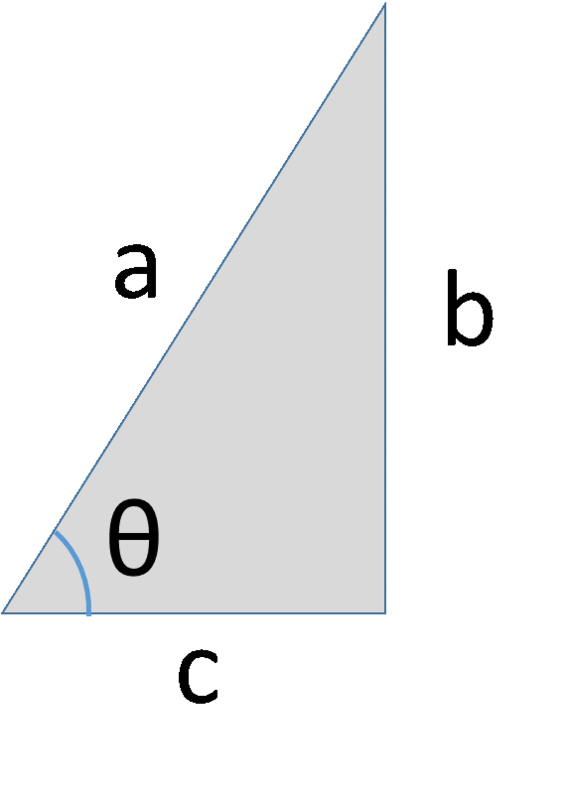
これらの間にはどんな関係性があるのでしょうか。まずは上の式を見てわかることからです。

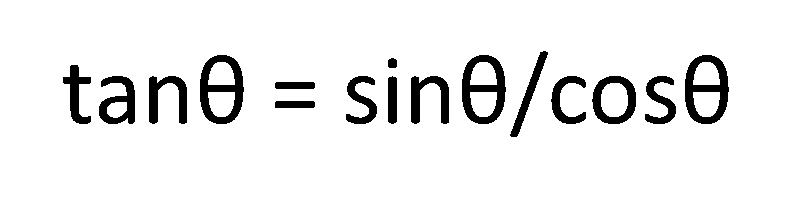
これはそれぞれの式にa,b,cを代入すれば分かります。

(sinθ)/(cosθ)=(b/a)/(c/a)=b/c=tanθ

次にこの式！これは非常に重要な式なので覚えましょう！

この式は三平方の定理から求めることができますが、ここでは割愛します。教科書を見ておきましょう。
最後に上の式をcos²θで割ると

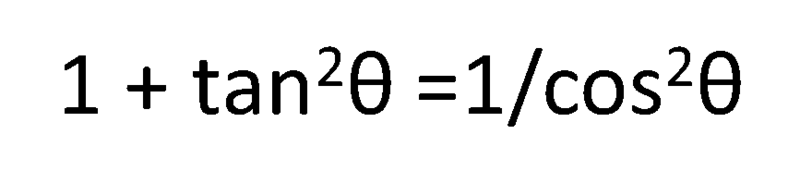
となります。

たった3つだけです。これらの式を使えば、sinθの値からcosθ、tanθの値が計算できますね。他も場合も同様です。ぜひ問題演習を通じてこの式が使いこなせるようにしましょう！

直角三角形ではない場合の三角比の使い方

こんにちは！今回で三角比も3回目です。前回までは三角比を「直角三角形の辺の比」として扱ってきました。でも、それでは三角比は直角三角形でしか使えません。そこで今回から直角三角形でない場合の三角比を定義してい、使える場面を増やします。この考え方は数学Ⅱの三角関数でも使うことになるので、しっかり押さえておきましょう！

今までは直角三角形で定義していましたが、それだとθは0~90°でしか適応できません。θが90°以上であった時にも、三角比が使えるようにここで新しい定義を導入します。

この定義を導入することで、θが90°以上でも適応できます。ただ、すこしわかりづらいですね…。そこでr=1とすることでもっと考えやすくなります。

これだと、cosθがx座標、sinθがy座標、tanθが直線の傾きとなって分かりやすいですね。この考え方でθについての方程式

を解いてみましょう！上の定義にしたがって図を描くと下図のようになります。

右上の直角三角形よりθ＝60°,120°となります。θ=120°も解の1つであることに注意しよう！

今回の内容は、今後三角比、三角関数を学習する上で非常に重要な考え方になります。しっかり理解できてから次へ進みましょう。

センター試験で頻出！正弦定理と余弦定理ってなに？

今回から、正弦定理と余弦定理について扱います。これらの定理は、辺の長さと角度の関係を数式で表した重要な定理です。しっかり理解して使いこなせるようにしましょう！今までよりちょっと難しくなりますが、センター試験でよく出題もされるので頑張っていきましょう！

正弦定理

まず、正弦定理がどのような定理なのか見てみましょう。

△ABC において、BC = a, CA = b, AB = c, 外接円の半径を R とすると、

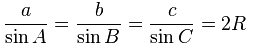
が成り立つという定理です。

証明も大事ですが、使い方はさらに大事です。簡単な例題で使い方を確認してみましょう。(証明が気になる人は教科書で確認！結構難しいですよ…)

例題
△ABCにおいて、a=10, B=60°,　C=75°のとき、bを求めよ。

解答

A+B+C=180°であるから、

A=180-(60+75)=45°

となる。正弦定理より

よって、

となります。もう一題！

△ABCにおいて、a=6, A=30°のとき、外接円の半径Rを求めよ。

正弦定理より

よって、

と求められます。

正弦定理では、三角形の1辺の長さとその両端の角の大きさが与えられた場合に、残りの2辺の長さを求めることができます。

余弦定理

これも、初めに定理がどのようなものか見てみましょう

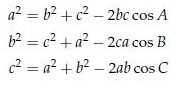
こちらも証明は大事ですが(気になる人は教科書で！)、使い方の方がさらに大事なので、簡単な例題で使い方を確認してみましょう。

△ABCにおいて、b=2, c=3,　A=60°のとき、aを求めよ。

余弦定理より

a²=b²+c²-2bccosA=2²+3²-2･2･3cos60°=7

となります。

また、余弦定理の式より次の式が成り立ちます。

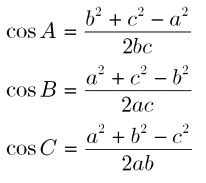
こちらもよく使う式になるので覚えておきましょう！

余弦定理では、三角形の2辺の長さとその間の角が与えられたとき、もしくは全ての辺の長さが与えられたときに使うことができます。

正弦定理と余弦定理、少し難しかったかもしれませんが使いこなせれば、角度と辺の長さの関係を結び付けることができるのです。しっかり理解しましょう。冒頭でも言いましたが、センター試験頻出分野です！！

正弦定理を使った面積の求め方

今回で三角比は最後です。今回の記事は三角比も出てきますが、おまけみたいな記事なのであっさり読めると思います。扱うテーマは面積・体積の求め方です。知っている公式もあると思いますが、知らないものは吸収して自分の武器にしていきましょう！

まず、三角形の面積公式です。皆さんが今までに知っている三角形の公式は

(底辺)×(高さ)×1/2

だと思いますが、三角比を使って求めることも出来るのです。

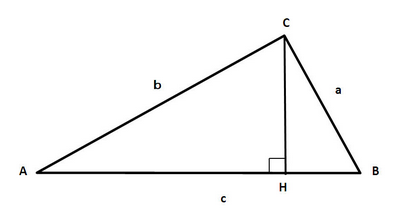
三角形の面積をSとしたときに

とすると求めることができるのです！

三角形ABCの面積Sは「底辺×高さ÷２」なので

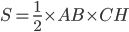         …①

で求めることができます。

ここで三角形ACHについて考えてみましょう。

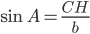
より

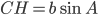
ということがわかります。

これを①の式に代入すると

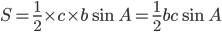
となり、公式を導きだすことができます。

今回のメインテーマはこれで終わりなので(笑)、面積や体積について、もう少し紹介します！

まずは、半径rの球の体積Vと表面積Sを求める公式です。

です。こちらは証明に微積が関わってくるので、証明は省略します。数学Ⅲで微積をマスターしたらぜひ挑戦してみてください！

最後に相似な図形の面積比・体積比について、簡単に紹介します。

相似比が2:3の図形の面積比は4:9 に体積比は8:27になります。すなわち面積比は2乗の比、体積比は3乗の比となるのです。

これで5回にわたってやってきた三角比を終了したいと思います。5回分読んで理解ができていれば、"使える"形になっているので、問題演習を通じて三角比を自分の武器にしましょう！

「数学が苦手だけど、どこから始めればいいか分からない」そんな受験生が数学の成績を大学受験の基礎から伸ばすためにおすすめの参考書をご紹介します！

> 京大生が使ってた！？マセマの「初めから始める」で伸ばした数学の勉強法 - イクスタ