今回で三角比は最後です。今回の記事は三角比も出てきますが、おまけみたいな記事なのであっさり読めると思います。扱うテーマは面積・体積の求め方です。知っている公式もあると思いますが、知らないものは吸収して自分の武器にしていきましょう！

まず、三角形の面積公式です。皆さんが今までに知っている三角形の公式は

(底辺)×(高さ)×1/2

だと思いますが、三角比を使って求めることも出来るのです。

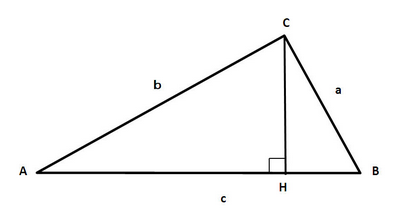
三角形の面積をSとしたときに

とすると求めることができるのです！

三角形ABCの面積Sは「底辺×高さ÷２」なので

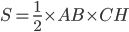         …①

で求めることができます。

ここで三角形ACHについて考えてみましょう。

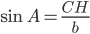
より

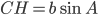
ということがわかります。

これを①の式に代入すると

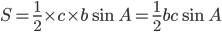
となり、公式を導きだすことができます。

今回のメインテーマはこれで終わりなので(笑)、面積や体積について、もう少し紹介します！

まずは、半径rの球の体積Vと表面積Sを求める公式です。

です。こちらは証明に微積が関わってくるので、証明は省略します。数学Ⅲで微積をマスターしたらぜひ挑戦してみてください！

最後に相似な図形の面積比・体積比について、簡単に紹介します。

相似比が2:3の図形の面積比は4:9 に体積比は8:27になります。すなわち面積比は2乗の比、体積比は3乗の比となるのです。

これで5回にわたってやってきた三角比を終了したいと思います。5回分読んで理解ができていれば、"使える"形になっているので、問題演習を通じて三角比を自分の武器にしましょう！

Part1 :　https://www.ikstudie.com/articles/237
Part2 :   https://www.ikstudie.com/articles/247
Part3 :　https://www.ikstudie.com/articles/249
Part4 :   https://www.ikstudie.com/articles/256