第１章では、方程式の基礎となる展開についてです。
展開とは”複数の多項式で表された式を１つの多項式で表す”ことです。
難しいことを言ってるなと思っている人も多いと思います。
ですが、式で見てみるとそんなに難しくはありませんよ！

ちなみに前回の記事はこちらです！
今から始める！本当に数学が苦手な人への方程式！[0章]

①           a(b+c)=ab+ac

こんなのや、

②           (a+b)(c+d)=ac+ad+bc+bd

こんなのです。分配法則と言われるものです。見たことある人もいるのではないでしょうか？

もっと丁寧にこの式の解説をすると、

①

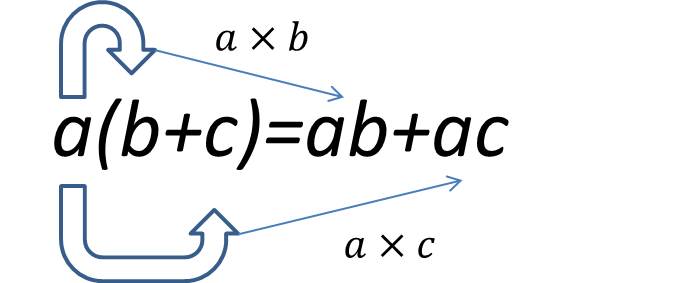
これは割とわかりやすいですね！カッコの前のaがカッコの中のbとcの両方にかけられています。もちろん、マイナスの符号がついていた場合には符号が変わってきます。間違いやすいのが、aにマイナスの符号がついていた場合のかけ忘れです。

 

②

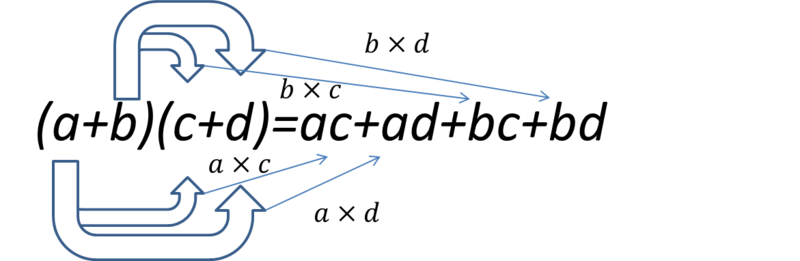
②はカッコのついた多項式同士のかけ算です。少し複雑にも見えますが、この式での展開のかけ算は上記の4通りしかありませんし、基本のやっていることは①のときと変わっていません。aをcとd両方にかけ、bもcとdの両方とかけるだけです。この場合にも符号には気を付けてください！

 

以上が基本的な展開の考え方でした。次は実践的な問題を使って説明していきたいと思います。

(x+6)(x+2)=＿＿＿＿

このような問題です。よく見かける、xの多項式同士の展開です。このような2つの多項式に同じ文字が用いられている場合には、以下のような展開の仕方があります。

①

 

②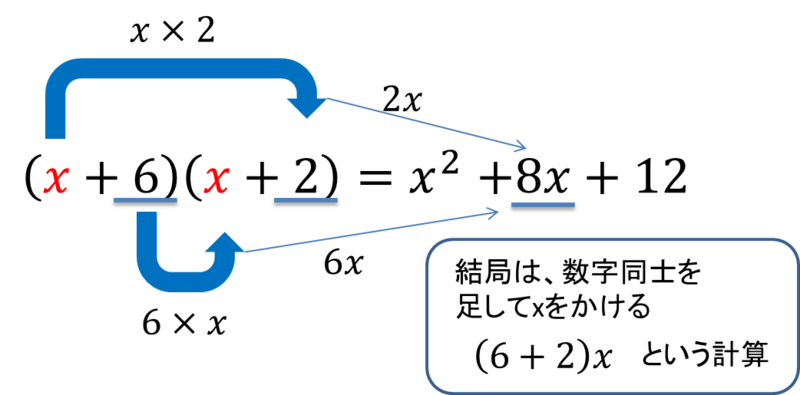

 

③

先ほどのやり方通りにやっていっても答えを出すことはもちろんできますが、いちいち展開を行っているのは時間がかかってしまいます・・・

そこで、上のようなxの多項式同士の展開の場合には、

              ①：x×x　（xの2乗の項）

              ②：(6×2) x　（xの項）

              ③：6×2　（xを含まない定数の項）

というようになります。これを一般形で表すと、

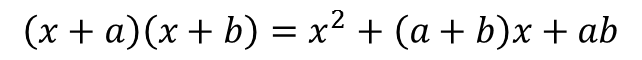
このような式になります。この式は単に暗記するのではなくパッと見で展開できるようになるくらいまで慣れるくらいにしておいてください。どのように慣れていくかというと、やはり、計算練習を繰り返していくしかありません。

 

また、

(2x+3)(3x—4)=＿＿＿＿

このような式の展開にも慣れておきましょう。今回の場合では上の赤い四角で囲った式を用いるだけでは展開はできません。xの2乗の項（xの係数には気を付けて！）とxを含まない項に関しては同様の計算ができますが、xの項の計算が少し違います。そして、後ろのカッコの中の”‐4”にも注意しましょう！

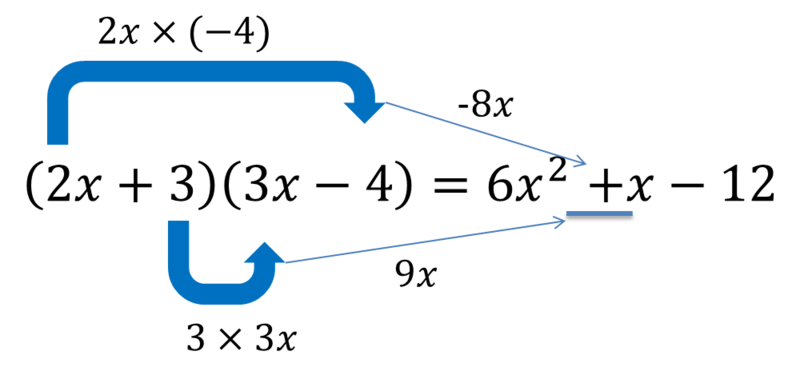
このように、内側同士、外側同士をかけて足すことでxの項を求めることができます。そんなに難しい計算ではないですが、今回のように負の符号が出てきている場合には符号に気を付けてください。

 

今回も、何問か計算の練習をしてみましょう！このような計算問題はやればやるほど必ずできるようになります。どんどんいろんな問題にチャレンジしてみましょう！

 

①           (2x+4)(4x+5)

②           (—3x+2)(2x—4)

③           (—2x—3)(—6x+4)

④           (7x—4)(—8x+3)

 

 

 

 

 

 

[解答]

①           (2x+4)(4x+5)=8x²+26x+20

 

②           (—3x+2)(2x—4)=—6x²+16x—8

 

③           (—2x—3)(—6x+4)=12x²+10x—12

 

④           (7x—4)(—8x+3)=—56x2+53x—12

 

次はこちらへ！
今から始める！本当に数学が苦手な人への方程式！[2章]