今回から、正弦定理と余弦定理について扱います。これらの定理は、辺の長さと角度の関係を数式で表した重要な定理です。しっかり理解して使いこなせるようにしましょう！今までよりちょっと難しくなりますが、センター試験でよく出題もされるので頑張っていきましょう！

まず、正弦定理がどのような定理なのか見てみましょう。

△ABC において、BC = a, CA = b, AB = c, 外接円の半径を R とすると、

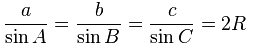
が成り立つという定理です。

証明も大事ですが、使い方はさらに大事です。簡単な例題で使い方を確認してみましょう。(証明が気になる人は教科書で確認！結構難しいですよ…)

例題
△ABCにおいて、a=10, B=60°,　C=75°のとき、bを求めよ。

解答

A+B+C=180°であるから、

A=180-(60+75)=45°

となる。正弦定理より

よって、

となります。もう一題！

△ABCにおいて、a=6, A=30°のとき、外接円の半径Rを求めよ。

正弦定理より

よって、

と求められます。

正弦定理では、三角形の1辺の長さとその両端の角の大きさが与えられた場合に、残りの2辺の長さを求めることができます。

これも、初めに定理がどのようなものか見てみましょう

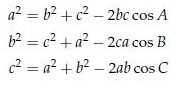
こちらも証明は大事ですが(気になる人は教科書で！)、使い方の方がさらに大事なので、簡単な例題で使い方を確認してみましょう。

△ABCにおいて、b=2, c=3,　A=60°のとき、aを求めよ。

余弦定理より

a²=b²+c²-2bccosA=2²+3²-2･2･3cos60°=7

となります。

また、余弦定理の式より次の式が成り立ちます。

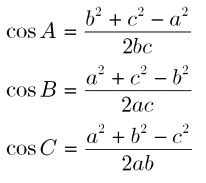
こちらもよく使う式になるので覚えておきましょう！

余弦定理では、三角形の2辺の長さとその間の角が与えられたとき、もしくは全ての辺の長さが与えられたときに使うことができます。

正弦定理と余弦定理、少し難しかったかもしれませんが使いこなせれば、角度と辺の長さの関係を結び付けることができるのです。しっかり理解しましょう。冒頭でも言いましたが、センター試験頻出分野です！！

Part1 :　https://www.ikstudie.com/articles/237
Part2 :   https://www.ikstudie.com/articles/247
Part3 :　https://www.ikstudie.com/articles/249