【物理徹底解説】力学単振動を完全攻略①~公式チェック編
こんにちは!東大生のフッシーです。みなさん、物理の勉強は進んでいますか?物理の力学分野では単振動が最も頻出の分野だと思いますが、この単振動、全然わからないという受験生も多いのではないでしょうか。
私も受験生だったとき、はじめは全く単振動がわからず模試などで出されるとお手上げだったのですが、夏に猛勉強することで解き方のコツをつかみ、秋には模試の単振動の分野でほぼ満点を取るまでになりました。
そこで、今回から二回に分けて単振動の問題の解き方をわかりやすく解説したいと思います。
今回の記事では単振動の押さえるべき公式を説明します。具体的な解き方は次の記事で書くので、公式をすべて覚えている方は今回は読み飛ばしていただいてかまいません!
等速円運動
単振動を理解するためにはまず等速円運動を理解する必要があります。そのため、まずは等速円運動について解説いたします!

(画像出典 受験の月)
等速円運動とは読んで字の通り、速さが一定の円運動です。常に物体の運動方向と垂直な方向に一定の大きさの力をかけると、物体は等速円運動します。
円の半径をr、運動の角速度(一秒あたりに何rad回転するか)をωとおくと、

となります。速度の向きは円の接線方向、加速度と力の向きは円の中心方向となります。この力は常に中心を向いているため向心力と呼ばれ、大きさは

となります。
単振動と等速円運動の関わり
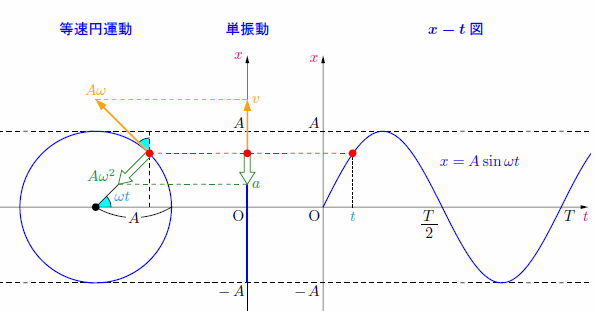
では、この等速円運動が単振動とどうかかわってくるのでしょうか。実は、単振動とは等速円運動の正射影にあたる運動(つまり、等速円運動を真横から見た運動)なのです!
(画像出典 受験の月)
今回はt=0のとき単振動の中心(x=0)に物体があるとします。また、図一では円の半径がrだったのが、図二ではAになっていますね。
単振動ではAを振幅、ωを角速度といいます。また、座標、速度、加速度は図よりそれぞれ

となります。tでxを微分したものがv、vを微分したものがaとなるので、xだけ覚えれば大丈夫です!また、速さは振動の端で0、振動の中心で最大となり、加速度の大きさは振動の端で最大、振動の中心で0となることを押さえておきましょう!
さて、運動方程式より、F=mα=-mω²xとなりますね。ここで、定数であるmω²をKとおくと上の式は
F=-Kx
となります。(このFは復元力と呼ばれます。)このような式であらわされる運動が単振動なのです!(x>0のとき負の方向に力がかかり、x<0のとき正の方向に力がかかるため振動がおこるのです。)この事実は非常に重要なので絶対に頭に叩き込んでください!
また、mω²=Kを変形することで角速度と周期は

となります。
単振動のエネルギー保存則
位置エネルギーmghとは、保存力である重力の仕事をエネルギーとして表したものでしたね。実は、単振動の復元力も保存力であるため、復元力の仕事を位置エネルギーとして表すことができるのです!その位置エネルギーは

です。したがって、エネルギー保存則は
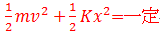
となります。
以上の公式を用いることで、だいたいの単振動の問題は解けてしまいます。上で赤で書かれたところは超重要ですので、絶対に覚えてくださいね!それでは、次の記事ではいよいよ単振動の問題の解き方を解説します!
大学受験生で物理を使う受験生におすすめの記事
> 【物理・力学編】公式一覧とその覚えるコツまで、これでアナタも力学マスター



物理




